문자열 키의 map, unordered_map 성능 비교
map 과 unordered_map 은 키, 값을 저장할 수 있는 컨테이너다. map 은 Red-Black Tree 를 사용해 키의 순서를 유지하는 반면 unoredered_map 은 해시 테이블을 사용해 키의 순서를 유지하지 않는다. unordered_map 은 키의 순서를 유지할 필요가 없기 때문에 탐색 속도등에 유리한 점을 가질 수 있다. (아래 그림 좌: Red-Black Tree, 우: Separate Chaining Hash Table)
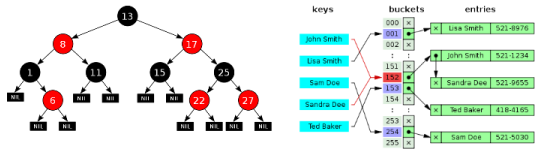
데이터가 N 개일 때 map 은 O(lgN) 의 탐색 속도를 보이고 unordered_map 은 O(1) 의 탐색 속도를 보인다. 때문에 데이터가 많을 수록 unordered_map 이 속도에 유리한데 문제는 “언제부터 유리한가?” 이다. 특히 키가 문자열일 때는 어떤 차이가 발생하는지가 궁금해 몇 가지 테스트를 해보았다. (문자열에 대한 궁금증은 지난번 Static String Table Lookup using Radix Tree의 벤치마크 결과 때문이다)
Map, Unordered_map<int, …>
먼저 다음과 같이 int 를 키로 받는 map, unordered_map 타입의 변수를 준비한다.
std::map<int, int> map;
std::unordered_map<int, int> umap;
struct bypass {
size_t operator()(int v) const {
return (size_t)v;
}};
std::unordered_map<int, int, bypass> umap_raw;
unordered_map 의 경우 두 개를 만들었는데 하나는 hash 함수로 기본 hash<int> 를 사용하는 것과 나머지 하나는 키 값을 그대로 해시 값으로 사용하는 것이다. VC++ 의 unordered_map 은 해시값으로 부터 버킷을 찾아낼 때 해시값의 하위 b 비트를 보는 형태로 구현되어 있어서 키에 대한 hash 값의 하위 b 비트의 분포가 고른지가 중요하다. 때문에 기본 hash<int> 는 입력값의 하위 b 의 분포가 고르지 않더라도 그것을 고르게 만드는 역할을 한다. 하지만 입력 데이터의 키의 하위 b 비트가 애초부터 고르다면 그대로 해시값으로 쓰는 것도 고려해볼만 하다. 이를 확인하기 위해 hash<int> 사용 umap 과 bypass 사용 umap_raw 이렇게 2개를 만들었다.
다음은 데이터 N 개를 컨테이너에 넣고 탐색을 한다. 테스트는 간단히 [0, N) 범위의 정수를 키로 넣고 그 키들을 다시 탐색하는데 얼마나 걸리는지를 측정했다.
Test<T>
{
T dict;
for (int i=0; i<N; i++)
dict.insert(make_pair(i, i));
// Measure Elapsed Time
for (int i=0; i<N; i++)
dict.find(i);
}
그 결과는 다음과 같다. (실행 환경: Intel i7-3550 3.3GHz, Windows 7 SP1, VC++ 10 SP1) X 축은 데이터 크기 N, Y 축은 탐색 1회에 걸린 시간 µs 이다.
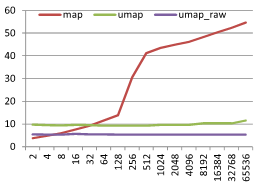
먼저 map은 O(lgN) 의 형태를 보이는 것을 알 수 있다. 다만 128~512 구간에서 급격히 느려지는데 이는 캐시 미스의 영향으로 보인다. unordered_map 은 hash<int> 와 bypass 모두 O(1) 의 형태를 보인다. 특히 bypass 는 hash 단계에 시간을 소모하지 않아 hash<int> 에 비해 2배 빠른 것을 볼 수 있다. 이 그래프로 부터 hash<int> 을 사용했을 때는 N 이 32 부터, bypass 를 사용할 때는 N 이 6 일 때 부터 unordered_map 이 map 보다 탐색에 유리한 것을 알 수 있다. (다만 이 magic number 는 컴파일러, STL, 실행 환경에 종속적이니 참고에 주의해야 한다.) 그렇다면 문자열이 키인 경우에는 어떨까?
Map, Unordered_map<const char*, …>
키로 넣을 문자열 집합을 정의하자. 먼저 문자열 길이를 M 이라 하고 문자열을 구성하는 문자 집합을 A 라고 한다. 예를 들어 문자열 길이 M=4, 문자 집합 A={0..9, A..F } 에 해당하는 문자열들의 예는 다음과 같다.
- 0000 1101 … 9A8E 9A8F … FFFF
이 집합에서 사전식 순서로 전체 집합에서 균일한 간격을 가지는 데이터 4개를 뽑으면 다음과 같은 문자열을 고를 수 있다.
- 0000 5555 AAAA FFFF
만약 동일한 집합에서 32 개를 뽑으면 다음과 같은 문자열을 고를 수 있다.
- 0000 0842 1084 18C6 … E738 EF7A F7BC FFFF
일반화 시키면 길이가 M 인 문자열 집합에서 N 개의 문자열을 뽑을 때는 사전식 순서로 번호를 매긴 문자열 리스트에서 0, A^M/(N-1), 2*A^M/(N-1) … A^M-1 번 째 문자열을 키로 사용한다고 할 수 있다.
이렇게 고른 키를 가지고 다음과 같은 map 과 umap 에 키, 값을 등록한다.
struct less_str {
bool operator () (const char* a, const char* b) const {
return strcmp(a, b) < 0;
}};
std::map<const char*, int, less_str> map;
struct hash_str {
size_t operator()(const char* s) const {
size_t v = 0;
while (char c = *s++) {
v = (v << 6) + (v << 16) - v + c;
return hash<int>()(v);
}};
struct equal_str {
bool operator () (const char* a, const char* b) const {
return strcmp(a, b) == 0;
}};
std::unordered_map<const char*, int, hash_str, equal_str> umap;
unordered_map 의 hash 함수로 sdbm 해시 함수를 사용했다. 그리고 그 결과를 바로 hash 값으로 사용하지 않고 hash<int> 를 한 번 더 실행해 사용했다. 왜냐하면 sdbm 해시 함수가 하위 b 비트의 균일성을 보장해주지 않기 때문이다. 이제 준비가 되었으니 아래와 같이 탐색!
Test<T>
{
T dict;
for (int i=0; i<N; i++)
dict.insert(make_pair(k[i], i));
// Measure Elapsed Time
for (int i=0; i<N; i++)
dict.find(k[i]);
}
결과는 아래와 같다. M 이 4, 8, 12, 16 의 경우를 테스트했고 X 축은 데이터 크기 N 이고 Y 축은 탐색 1회에 걸린 시간 µs 이다.
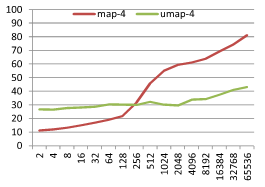
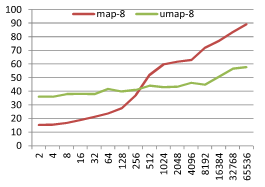
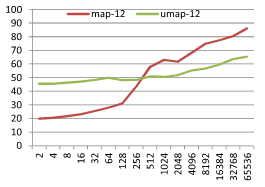
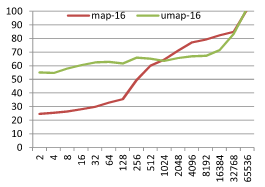
기본적으로 정수가 키인 경우와 비슷한 결과를 보인다. 하지만 M 의 크기 변화에 따라 재미있는 현상이 발생하는데 map 과 unordered_map 의 성능이 교차하는 점이 M 이 커짐에 따라 같이 커지는 현상이다. 이를 좀 더 잘 보기위해 M 에 따라 map 탐색시간 / unordered_map 탐색시간 비율 그래프를 아래와 같이 그려봤다.
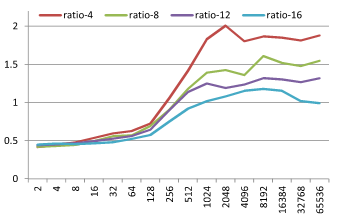
M=4 일때 ratio 가 1이 되는 지점은 N=128~256 지점이고 M=16 일때 ratio 가 1이 되는 지점은 N=512~1024 지점이다. M 이 커질 수록 map 이 유리한 N 의 범위가 커지는 것을 볼 수 있다. 왜그럴까?
시간 복잡도
map 와 unordered_map 의 “문자열 단위” 탐색 작업의 시간 복잡도는 다음과 같다.
- map:
- 노드 마다 문자열 비교: O(lgN)
- 마지막 노드의 문자열 비교: O(1)
- unordered_map:
- 입력 문자열의 hash function 수행: O(1)
- 입력 문자열과 버킷에 있는 문자열 비교: O(1)
이번에는 문자열 길이를 적용해 “문자 단위” 탐색 작업의 시간 복잡도를 계산해보자.
- map:
- 노드 마다 문자열 비교: ?
- 마지막 노드의 문자열 비교: O(M)
- unordered_map:
- 입력 문자열의 hash function 수행: O(M)
- 입력 문자열과 버킷에 있는 문자열 비교: O(M)
map 의 노드 마다 문자열을 비교하는 부분의 시간 복잡도를 구해보자. map 을 구성하는 트리가 완전하게 균형된 트리를 구축했다고 했을 때 M=4 의 트리는 다음과 같은 형태를 가진다.
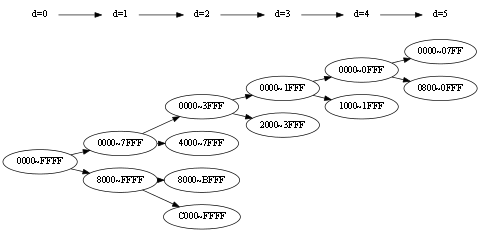
먼저 키로 받은 데이터 분포 특성에 의해 d=0 노드는 첫 글자 만으로 분기가 가능하다. 이 부분이 중요한데 노드 분기를 위해 문자 M 을 모두 비교할 필요가 없기 때문이다. d=4 노드부터 두번째 문자까지 비교를 해야 한다. 이를 일반화 하면 노드 깊이 d 일 때 분기를 위해 필요한 문자 비교 횟수는 다음과 같다.
첫 노드부터 마지막 노드까지의 비교 횟수의 합은 다음과 같다.
따라서 비교에 필요한 횟수는 길이 M 과 관계 없이 N 에 종속적인 것을 알 수 있다. (이것은 키 문자열 집합의 분포 특성 때문에 그렇다)
map 과 unoredered_map 을 N 과 M 의 시간 복잡도로 표시하면 다음과 같다. (문자 단위)
- map: O(lgN^2) + O(M)
- unordered_map: O(M) + O(M)
map 은 M 의 길이에 덜 반응하고 unordered_map 은 M 의 길이에 그대로 반응하기 때문에 M 이 커짐에 따라 map 보다 unordered_map 의 속도 저하가 커질 수 있다. 하지만 위의 분포는 다소 인위적인 분포이며 실제 키 문자열 집합이 이러한 이상적인 분포를 가지는 경우는 드물다. 하지만 대부분의 데이터는 어느정도 이런 형태를 유지하는데 예를 들면 기본 컬러 16 의 이름은 다음과 같다.
- black, blue, cyan, gray, green, lime, magenta, maroon, navy, olive, purple, red, silver, teal, white, yellow
이 집합은 N 이 16 이고 |A|=26 이기 때문에 모든 노드에서 첫번째 문자만으로 분기가 가능해야 한다. 하지만 (black, blue), (gray, green), (magenta, maroon) 의 경우에는 세 번째 문자까지 봐야 구분이 가능하다. 그럼에도 불구하고 특정 문자열 X 가 주어졌을 때 이 X 가 노드 분기에 필요한 문자 비교 횟수는 대부분 1이다. (예를 들어 magenta 가 주어졌을 때 maroon 을 제외하고는 모두 비교 횟수 1이다) 따라서 이 문자열 집합도 map 이 unordered_map 보다 탐색 속도에 우위를 가지게 된다. 하지만 만약 문자열의 형태가 아래와 같이 접두사가 비슷한 경우라면 비교 문자 개수가 크게 늘어나 전혀 다른 양상을 보인다.
- abnormal abnomality abnomalities abnormalization
결론
몇가지 테스트를 해서 정리를 해보면 이렇다.
- map, unordered_map 의 탐색 속도는 데이터 크기 N 이 작을 때는 map 이 클 때는 unordered_map 이 유리하다.
- map 은 데이터 크기 N 이 커짐에 따라 unordered_map 보다 캐시 미스의 영향을 더 빨리 받는다. 이것은 map 이 탐색을 위해 여러 노드를 방문해야 하기 때문으로 보인다.
- unordered_map 은 해시 함수의 성능이 중요하다. 특히 VC++ 의 경우에는 하위 b 비트의 고른 분포가 중요하다.
- 문자열 키를 사용하는 경우 정수 키를 사용하는 경우에 비해 map 이 더 큰 N 까지 탐색 성능 우위를 가진다. 이것은 문자열 비교에 적은 비교 횟수를 필요로 하기 때문이다.
- 따라서 문자열 길이가 길고 데이터 크기가 크지 않은 경우에는 map 이 unordered_map 보다 탐색에 유리하다.
map 도 좋고 unordered_map 도 좋다. 왜 이렇게 unordered 치는데 오타가 나는지는 모르겠지만…